什么是计算复杂度?
在计算机科学中,计算复杂度是衡量算法性能的指标之一。它描述了随着输入数据规模的增加,算法所需的计算资源(时间和空间)的增长情况。计算复杂度的目标是评估算法在处理大量数据时的效率,帮助开发者选择适当的算法来解决问题。通过了解和应用计算复杂度,我们可以更好地选择和设计算法,提高程序性能,优化资源利用,并在不同问题场景下做出明智的决策。
计算复杂度不仅可以帮助我们衡量和比较不同算法的效率,还有以下几个重要作用:
算法选择: 在解决同一个问题时,可能存在多种不同的算法。通过比较它们的计算复杂度,我们可以选择性能最优的算法,从而提高程序的执行效率。
性能优化: 知道一个算法的计算复杂度,我们可以针对其瓶颈部分进行优化,以减少时间和空间的消耗,从而提升整体性能。
资源预测: 预先估计算法在不同数据规模下所需的资源,有助于规划硬件资源、调整系统参数以适应不同的应用场景。
问题规模: 计算复杂度告诉我们算法的性能如何随问题规模的增加而变化。这对于预测算法在实际应用中的行为非常重要。
教育与研究: 在教学和研究中,计算复杂度是讨论算法效率的重要工具。它能够帮助理解算法性能,促进算法的改进和创新。
在接下来的部分,我们将深入探讨计算复杂度的不同方面,包括时间复杂度、空间复杂度、分析方法以及实际应用。
时间复杂度与空间复杂度
时间复杂度和空间复杂度是算法分析中不可或缺的两个概念。时间复杂度衡量了算法的执行时间随问题规模的变化情况,而空间复杂度则衡量了算法所需的额外内存资源随问题规模变化的情况。通过理解和应用这两个复杂度概念,我们可以更好地选择、设计和优化算法,以提高程序的执行效率,适应不同规模的数据处理需求。接下来,我们将深入探讨如何分析算法的时间复杂度和空间复杂度,以及如何将这些概念应用于实际问题。
时间复杂度:
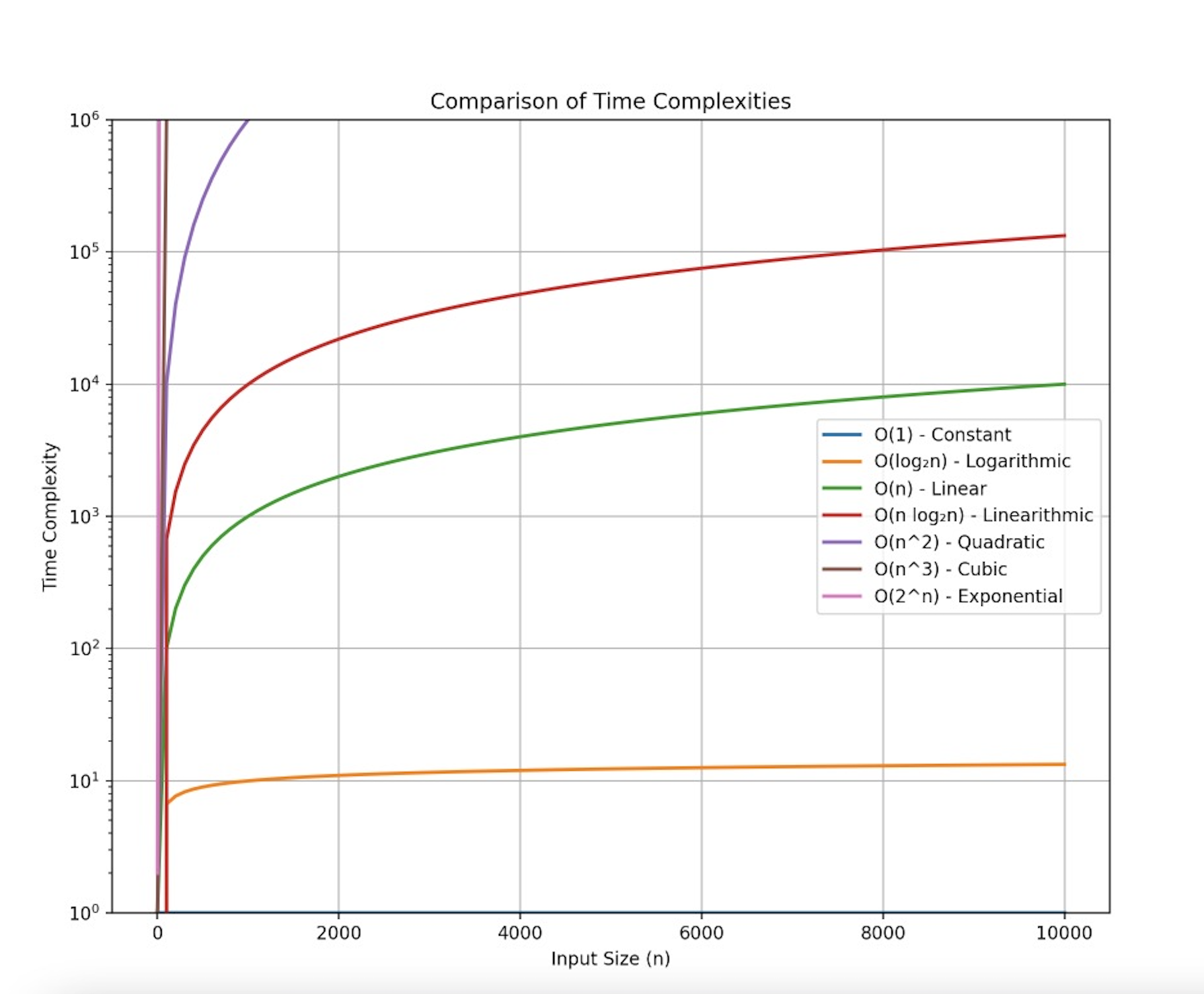
时间复杂度是衡量算法执行时间随输入数据规模增加而增长的程度。它是一个关于问题规模 n 的函数,表示算法所需执行基本操作的次数或步骤数。通常使用大 O 表示法来表示时间复杂度,例如 O(1)、O(log n)、O(n)、O(n log n) 等。
当规模n增长时,不同时间复杂度增长趋势,如图所示
时间复杂度在算法分析中具有重要的作用:
性能预测: 时间复杂度能够帮助我们预测算法在不同输入规模下的执行时间。这对于在实际应用中评估算法性能至关重要。
算法选择: 通过比较不同算法的时间复杂度,我们可以选择在给定问题中性能最佳的算法,从而提高程序的效率。
问题规模: 时间复杂度告诉我们随着问题规模增加,算法的执行时间如何变化。这有助于理解算法适用的问题范围。
空间复杂度:
空间复杂度是衡量算法执行所需内存资源随输入数据规模增加而增长的程度。它也是关于问题规模 n 的函数,表示算法所需的额外内存空间。和时间复杂度类似,通常使用大 O 表示法来表示空间复杂度。
空间复杂度在算法设计和评估中也具有重要意义:
资源规划: 了解算法的空间复杂度有助于规划系统的内存资源,确保在大规模数据处理时不会出现内存溢出等问题。
内存优化: 知道哪些操作会消耗大量内存,我们可以针对性地优化算法,减少内存占用。
系统要求: 某些应用场景对内存的要求较高,空间复杂度能够帮助我们选择适合的算法,满足系统要求。
在接下来的部分,我们将深入探讨大 O 表示法作为计算复杂度的标准记法,并详细解释常见的时间复杂度,例如 O(1)、O(log n)、O(n)、O(n log n) 等。这将帮助我们更好地理解不同算法的性能特点。
大 O 表示法
大 O 表示法是衡量算法复杂度的标准记法,它描述了算法执行时间或空间随问题规模增加的上限增长趋势。通常使用大 O 表示法表示算法的最坏情况复杂度。例如,O(n) 表示随着输入规模 n 的增加,算法执行时间将线性增长。
常见时间复杂度:
O(1) - 常数时间复杂度
常数时间复杂度表示算法的执行时间与问题规模无关,即使输入数据增加,算法执行时间也保持不变。典型的例子是直接访问数组元素。
O(log n) - 对数时间复杂度
对数时间复杂度表示算法的执行时间与问题规模的对数关系。常见的应用场景是二分查找等问题,每次操作都将问题规模减半。
O(n) - 线性时间复杂度
线性时间复杂度表示算法的执行时间与问题规模呈线性关系。例如,遍历数组中的每个元素。
O(n log n) - 线性对数时间复杂度
线性对数时间复杂度表示算法的执行时间与问题规模和其对数之积呈线性关系。快速排序和归并排序是常见的 O(n log n) 算法。
O(n^2) - 平方时间复杂度
平方时间复杂度表示算法的执行时间与问题规模的平方关系。通常出现在嵌套循环中。
O(n^k) - 多项式时间复杂度
多项式时间复杂度表示算法的执行时间与问题规模的某个幂关系。其中 k 是常数。